The Hitchhiker's Guide to Vector Embeddings in Machine Learning (for Geographers)
This blog breaks down complex AI concepts using familiar geographic language, making vector embeddings easy to grasp for geographers. Join us for the Data Wranglers Hackathon for More
For those who thought this blog would dive into using vector embeddings specifically for geospatial workflows, stay with me. While we're not going deep into that today, we are using geospatial concepts to make the unfamiliar more familiar. In machine learning, vector embeddings refer to the process of mapping unstructured data into a high-dimensional space where its key features, or semantics, can be easily compared. This might seem like a stretch from geography at first glance, but the parallels are surprisingly intuitive.
The goal of this blog is to simplify and explain AI concepts using vocabulary that geographers already know. By using relatable geographic examples, the blog aims to make the complex concept of vector embeddings more accessible to geographers.
You might not realize it, but vector embeddings are all around us from Spotify playlist recommendations to Google search results to personalized item suggestions on Amazon. And given the hackathon happening next week at Geo for Good Dublin on using the Earth Engine Dataset Explorer released late last week, this topic is timely.
The tool itself uses vector embeddings to encode its main catalog, incorporate additional dataset information, and search for relevant Earth Engine datasets based on user queries. Happy exploring, and if you are interested join us as Data Wranglers for our Hackathon at Geo for Good Mini Summit in Dublin.
In a rush? Want to hear an audio summary instead, here’s an AI generated from the whole blog for you to listen to. But we hope you enjoy reading the sections
Geocoding and Vector Encoding - The Heart of Mapping
When we search for an address on Google Maps, it doesn’t inherently understand the human language used in that search. Instead, it translates or geocodes the address into a pair of geographic coordinates: latitude and longitude. These coordinates are numeric representations of a specific point on the Earth's surface.
Want to go even further than lat long, check out Plus codes project from Google a truly unique representation of every address into a single alpha numeric code.
In machine learning, there is a similar transformation when dealing with unstructured data (like text, images, or even audio) by encoding it into vector embeddings which are effectively numeric representations of the data in n-dimensional space. For example, when you convert a word into a vector in natural language processing, that word is now represented by a series of numbers that encode its meaning in relation to other words.
Learn more about vector stores and embeddings here incase you wanted to do a deep dive.
In the same way, geographic coordinates allow us to plot points on a map, vector embeddings allow us to plot words (or tokens) in a multi-dimensional space and can be multi modal so it can do the image with image and audio and video formats.

These models usually divide words or any input into chunks called Tokens for creating for embeddings similar to geographical gridding spaces.

And just as a geographic location with multiple attributes associated with a feature, embeddings in machine learning are n dimensional to to represent richer features.
The Geography of Distance - A Tale of Two Spaces
So you want to go from Point A to Point B , let’s stretch the mapping example and understand that more than one way to route you, including options like fastest route which usually translates to lesser time, most environmental friendly routes, routes to avoid tollways among other options. This is a simple task of calculating the distance between two sets of coordinates, typically using Euclidean distance in two dimensions (latitude and longitude).
Machine learning performs a similar task when comparing vector embeddings. Two embeddings that are close together in vector space represent similar data points. For example, two words that have similar meanings will have vectors that are close together, while words with different meanings will have vectors that are far apart.

The most common ways to calculate distance between vectors in machine learning include Euclidean distance, cosine similarity, and dot product. The choice of metric depends on the specific task at hand, but the principle remains: the closer two vectors are, the more similar they are in meaning or context.

In both cases geographic or machine learning vector space distance calculations allow us to perform meaningful comparisons. Whether you're determining proximity between cities or finding the most similar data points, you are working within an embedding space.
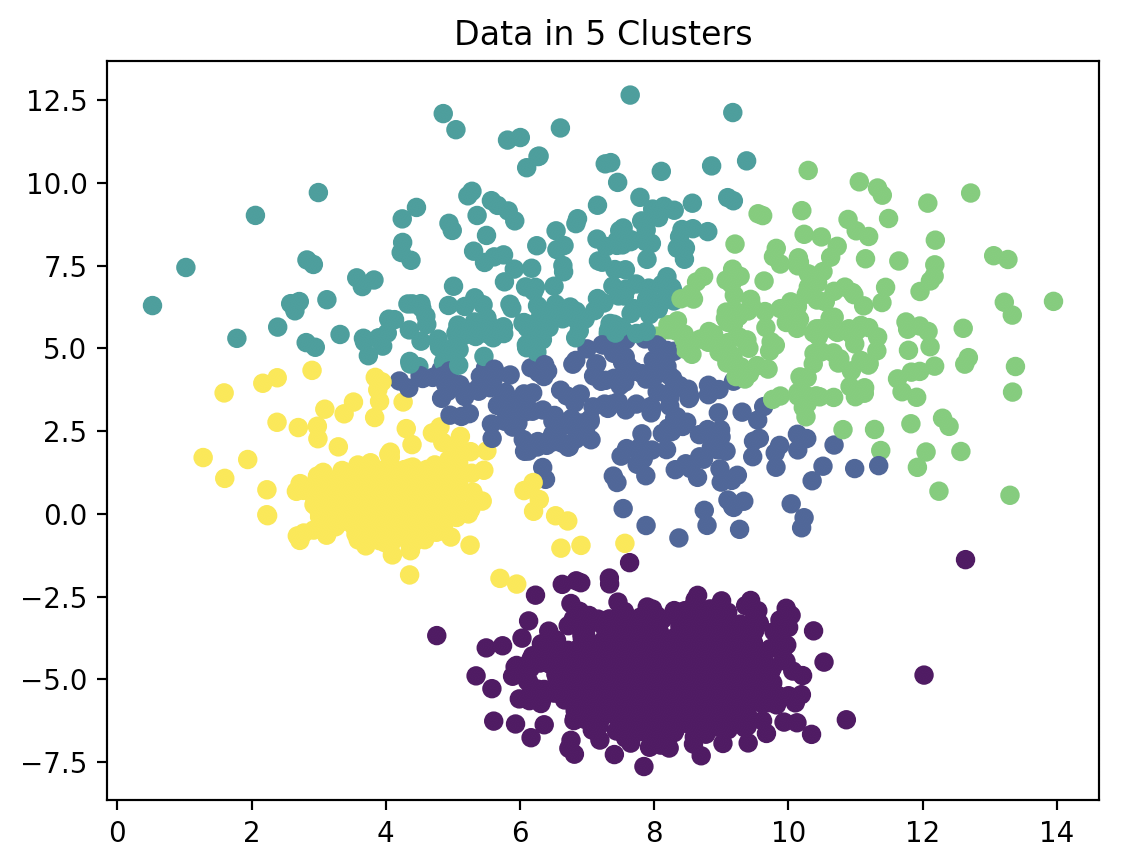
Clustering and K-Means: A Geographical Analogy
Geographers are familiar with clustering grouping together locations that share similar characteristics, such as population density, climate, or proximity to certain landmarks. Clustering algorithms, such as K-Means, are also common in geospatial analysis to find areas of interest or “hot spots.”
In the machine learning world, clustering is a fundamental concept that helps organize data points (or embeddings) into meaningful groups. For example, when you're clustering customer preferences or grouping similar pieces of text, you're trying to achieve the same goal: organizing data based on similarity. K-Means is a popular algorithm for this purpose in both geography and machine learning, where it groups vectors into clusters by minimizing the distance between points in each group and the group’s centroid.
Sometimes, powerful ideas and concepts get lost in translation, especially when we’re crossing disciplines like geography and machine learning. This blog attempts to bridge that gap by making the complex world of vector embeddings more familiar and approachable for geographers. By drawing parallels to well-known geospatial practices like mapping coordinates, calculating distances, and clustering regions we can see that vector embeddings, at their core, follow similar principles. The goal is to demystify this AI concept, so geographers can explore how their existing knowledge intersects with the exciting possibilities in machine learning.





Great post! This is really helpful for me, in fact, so I appreciate it!